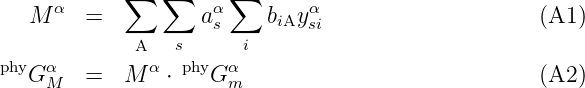
An attempt to document the status of the third generation unary database project for all interested
Bo Sundman April 8, 2021
This is an dynamic summary to keep everyone involved updated with the current development of the 3rd generation of the Calphad unary database. It also contains unresolved issues and ongoing discussions in Appendices.
The aim is to make the new thermodynamic databases closer to the physical reality while keeping them useful for demanding engineering applications which need rapid calculation of equilibria and various thermodynamic properties in multicomponent systems. The current unary database using the 1991 SGTE unary database by Dinsdale [7] will continue to be used in parallel for the foreseeable future.
Section 2 is a very short summary of decisions and unresolved issues, usually with a short motivation. We should keep this short and use the Appendices for detailed explanations, expressing different opinions and discussions.
At present the Appendices are mainly my personal view of things, but everyone should express their opinions there. All mistakes should also be recorded, otherwise we will make the same mistakes over and over again.
The sub projects are closely related, not independent.
This is a mandatory physical reality for all phases.
The entropy of perfect ordered crystalline phases at T = 0 K must be zero according to the third law. Such a phase must not have any terms depending on T with power ≤ 1 in its Gibbs energy expression.
The models by Qing [9] and Xiong [10] are accepted with minor modifications. This means separate Curie and Neel T but the proposal to have individual Bohr magneton number has been put on ice. Add some references of recent assessments!
The liquid two-state model proposed by Ågren [5] and more recently in Becker et al. [11] is used. A recent assessment of Al-C is by Zhangting et al. [16].
This model describe the amorphous and liquid phases with a single Gibbs energy function separated in two terms, GMamf and G Md.
The Equi-Entropy Criterion (EEC) proposed by Sundman et al. [15] is used to prevent the reappearance of crystalline solids extrapolated to high T. EEC replaces the breakpoint used in the SGTE 1991 unary database at the melting T of the solid phase of the pure elements by a software test of the entropy of solid and liquid phases. It has been used in the assessment by Zhangting et al. [16]
The fact that physical models has to be converted to moles per formula unit is explained in Appendix A. Modeling of thermal vacancies is discussed in Appendix G and molar volumes in Appendix H.
[1] Neumann, F. Untersuchung über die spezifische Wärme von Minaralien, Ann. Phys. Chem. 99 (1831) 1–39.
[2] Kopp, H. Über die spezifische Wärme der starren Körper, Ann. Chem. Pharmacie Suppl. 3 (1864) 289–342.
[3] Kaufmann, L and Bernstein, H Computer calculation of phase diagrams, (1970) Academic Press, New York, USA
[4] Hillert, M. Some viewpoints on the use of a computer for calculating phase diagrams Physica 103B 130B (1981) 31-40
[5] Ågren J, Thermodynamics of Suercooled Liquids and their Glass Transition Phys. Chem. Liq, 18 (1988) 123-139
[6] Tallon, J.L. A hierarchy of catastrophes as a succession of stability limits for the crystalline state, Nature 342 (1989) 658–660.
[7] Dinsdale, A, SGTE data for pure elements Calphad 15 (1991) 317-425
[8] Sundman, B, An assessment of the Fe-O system, J Phase Equil. 12 (1991) 127-140
[9] Chen, Q et al., Modeling of Thermodynamic Properties for BCC, FCC, Liquid and Amorphous Iron J Phase Eq. 22 (2001) 631-644
[10] Xiong, W et al., Magnetic phase diagram of the Fe-Ni system, Acta Mat. 59 (2011) 521-530
[11] Becker C. A. at al., Thermodynamic modelling of liquids: Calphad approaches and contributions from statistical physics Phys. Stat. sol., (2014) doi:10.1002/pssb.201350149
[12] Rogal, J et al., Perspectives on point defect thermodynamics Phys. Stat. sol., (2014) doi:10.1002/pssb.201350155
[13] Wang, P, Xiong, W, Kattner, U.R., Campbell, C.E., Lass, E.A, Kontsevoi, O.Y, Olson, G.B, Thermodynamic re-assessment of the Al-Co-W system Calphad, 59, (2014) 112-130
[14] Dinsdale, A et al. Use of third generation data for elements to model the thermodynamics of binary alloy systems: Part I - The critival assessment of data for the Al-Zn system, Calphad 68 (2020) 101723
[15] Sundman, B et al. A method for handling the extrapolation of solid crystalline phases to temperatures far above their melting point, Calphad 68 (2020) 101737
[16] Zhangting, H et al. The third generation Calphad description of Al-C including revisions of pure Al and C, Calphad 72 (2021) 102250
A model for the physical contribution to the Gibbs energy, phyG m, is normally per mole atoms indicated by the subscript m. However, the Gibbs energy models based on the compound energy formalism (CEF) [4], require the contribution per mole formula units of the phase. CEF use formula units because many phases contain vacancies or more complex constituents than the pure elements. In such a case the physical model function must be multiplied with the number of atoms/formula unit of the phase α,Mα, calculated as:
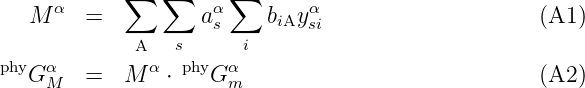
This fact has been ignored in earlier applications of the magnetic model resulting in nonphysical values of the Bohr magneton number for some phases, for example in the assessment of magnetite by Sundman [8].
Integrating the Einstein heat capacity model
where θ is fitted to experimental data for the elements gives a Gibbs energy:The Einstein model is preferred because it is simpler than any other model to integrate to a Gibbs energy. Even with a Debye model an additional polynomial in T is needed to describe the experimental data for each pure element.
The polynomial in T added to the Einstein function must not include terms with powers in T ≤ 1 or T ln(T).
It has been decided to use ln(θ) as composition dependent parameter. θ may possibly depend on P but must not depend on T.
In some cases a pure element, stoichiometric compound or endmember has its heat capacity fitted using multiple θ, for example pure C as graphite. A software provided function, GEIN(θ), with a single constant parameter, θ, can be used in the Gibbs energy expression for the endmember to calculate eq. B2 and its derivatives with respect to T for the endmember.
i) θ is an approximation of the phonon spectra,
ii) the heat capacity data for solutions are not well known and
iii) to avoid very complex modeling issues replacing linear T dependence in
other Gibbs energy parameters by θ parameters.
To do anything better than a single θ in solutions we should model the phonon spectra which is far outside the Calphad level of ambitions.
A single θ, normally representing the major phonon frequency, can be selected as the composition dependent θ used in the explicit Einstein contribution. This contribution must subsequently be subtracted from the Gibbs energy functions fitted with multiple θ for the endmember.
Evidently the 3rd law creates strong emotional argument. Some opinions below.
For the amorphous phase:
Consider a big piece of an amorphous system. Cut a large but finite part of this with N atoms. Call this piece A and consider it as a perfectly ordered unit cell. If A is repeated periodically we have a system with entropy 0 at T = 0 K. But we can also cut other parts in the big system, B, C, D etc all with N atoms. If any of these is repeated periodically we have a system with entropy 0 at T = 0 K. But this is not the case for an amorphous system. Instead it should be treated as a disordered system with parts A, B, C etc. This disorder means a finite entropy at T = 0 K. The larger the value of N the greater number of alternative parts B, C etc.
Another way to argue: the entropy S = kB ln(Ω) is a measure of the degree of disorder, Ω, i.e. the number of separate subsystems A, B, C etc. with practically the same energy. If N is large then Ω is also large but the number of subsystems, A, B, C etc. with N atoms in a given part of a large amorphous sample varies with 1/N. Thus there is a given entropy per atom in an amorphous sample.
Requiring that all phases, stable or metastable, must have S = 0 at T = 0 would mean Calphad cannot use its fundametal model, an ideal solution, because this will have S = ∑ ixi ln(xi) at T = 0. We can wait another 50 years until the 4th unary to introduce S = 0 for any other kind of phase if we find it possible and necessary.
Following a proposal from Dinsdale et al. [7] to avoid non-zero entropy at 0 K means that any linear T terms in the classical Kaufman lattice stabilities [3] (and several later papers) can be converted to a Δθ for the metastable phase to avoid non-zero entropy for the metastable phases of the pure elements.
Linear T terms in endmembers, excess parameters and other parameters contributing to the Gibbs energy can also be converted to a parameter in the composition dependence in θ. In principle a coefficient for a linear T term “b” can be replaced by “b/3R” in a θ parameter with the same composition dependence to reproduce the properties of the phase above θ.
Some care should be used to avoid negative θ.
The contribution to the Gibbs energy due to the magnetic properties per mole atom is:
where TC is the Curie or Neel T and β is the Bohr magneton number, all of which can vary with the composition. The magnetic contribution from eq. D1 is zero when either Curie or Neel T is negative.NOTE the current functions f(τ) etc. should be added.
The magnetic eq. D1 should be multiplied by Mα, see Appendix A, when used per mole formula unit.
There are separate Neel and Curie T and it is quite surprising to find that for a magnetic element the Neel and Curie T should have identical values but with opposite sign!
Individual Bohr magneton numbers for the elements is not adopted yet. The same Bohr magneton number is used for ferro- and antiferromagnetism as well as any kind of magnetic contribution.
...unfinished, some recent assessment references needed
The liquid phase is described using a two-state model described in Becker et al. [11].
This model has a Gibbs energy description including an Einstein heat capacity contribution for the metastable low T part of the liquid, GMamf, assumed to be an amorphous phase. It has also a parameter, GMd, describing both the transition to the liquid phase and the stable liquid above the melting T of the element:
In the amorphous state at low T the term exp(-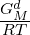 ) should approach zero (i.e. GMd
should approach very large positive values) and the second term in eq.E1 can
be ignored. For the stable liquid exp(-
) should approach zero (i.e. GMd
should approach very large positive values) and the second term in eq.E1 can
be ignored. For the stable liquid exp(-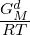 ) should be much larger than unity
(i.e. GMd should approach large negative values) and second term becomes:
) should be much larger than unity
(i.e. GMd should approach large negative values) and second term becomes:
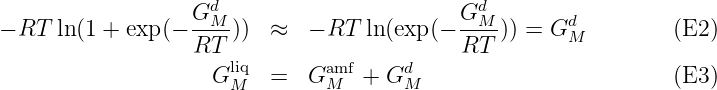
In the GMamf parameter one can use a linear T term because the amorphous phase may have nonzero entropy at 0 K. But no T ln(T) and no T powers less than 1 because the amorphous phase must have zero heat capacity at T = 0 K.
The GMd parameter should change from positive to negative values in the amorphous state and this can generate a heat capacity contribution. In the GMd parameter both linear T and T ln(T) terms are possible because they will not give any contributions at T = 0 K.
The parameters for the liquid two-state model, GMd, can be very different for elements with different melting T, for example Al and W [13]. Great care should be taken determining the GMd,
Composition dependent parameters for the stable liquid can be used in both GMd and GMamf but usually very little is known about the amorphous phase. Interaction parameters in the GMd can have linear a T term as it will not influence the low T properties.
The breakpoint at the melting T for the pure elements in the 1991 SGTE unary was an emergency fix to avoid that solid phases, which normally have an increasing heat capacity before melting, would become stable again when this increase is extrapolated to higher T. This will happen if the extrapolated heat capacity of the solid is larger than that of the liquid, which normally is fairly constant around 3R at high T. In the 1991 SGTE unary the heat capacity of the extrapolated solid was forced to approach that of the liquid above the breakpoint. The breakpoint represents a kind of 2nd order transition in the solid and it solved the primary problem but created others, for example strange heat capacity curves for compounds with their heat capacity modeled with the Neumann-Kopp rule [1, 2] and with higher melting T than a constituent element.
The similar breakpoint for the liquid, to avoid that the liquid becomes stable at low T, is removed by the liquid two-state model, see Appendix E. But there is no similar way to prevent the heat capacity of extrapolated solid to increase.
Instead a well established experience that the liquid is always the condensed phase with the highest entropy in a system, is used. This is a natural consequence of the fact that the liquid will become more stable than any solid phase at increasing T. An important observation is that this is independent of the phase compositions.
The Equi-Entropy Criterion (EEC) proposed by Sundman et al. [15] is based on this observation. During an equilibrium calculation EEC will compare, at the same T, the entropy of the solid phases with the entropy of the liquid at their current compositions. If a solid phase is found to have higher entropy than the liquid the conclusion is that this solid suffers from a bad extrapolation of its heat capacity and the solid Gibbs energy must also be wrong and the phase is not allowed to be stable.
EEC does not require any modification of the Gibbs energy expression of the extrapolation of the solid phase but must be implemented in the thermodynamic software using the data. No breakpoint is needed in the Gibbs energy function of the solid but some care should still be used to avoid that the heat capacity increases very rapidly above its melting T.
It is not forbidden to introduce a breakpoint in order to use the data in a software where EEC is not implemented but such a breakpoint should be at an even 100 K above the melting T, to indicate it is a fictitious breakpoint, and the derivative of the heat capacity should be continuous at the breakpoint to avoid the resemblance with a 2nd order transition.
During the discussions of EEC there were attempts to define a “crystalline breakdown T”, which should be a few 100 K above the melting T but it was found difficult to handle for solution phases and abandoned. EEC is related to the “entropy catastrophe” criteria [6] for a pure compound but it is applied to cases when the solid and liquid does not have the same composition. It is simply based on the experience that no solid phase can be stable with a higher entropy than that of the liquid at the same T.
All phases has defects of different kinds and the thermal vacancies are important for simulating kinetic properties. The Gibbs energy for thermal vacancies in a phase, GV a, should be:

There are several other proposals for thermal vacancies but it should be recognized that this energy is not related to vaporization or equilibrium with any other phase, most vacancies are created when atoms move to a grain boundary, dislocations or other crystalline defects.
The volume is not included in the 1991 unary database but is of great importance. Some ideas:
